Rmarkdown入门
胡华平
2019-04-20
自学材料:
R Markdown: The Definitive Guide(Yihui Xie, J. J. Allaire, Garrett Grolemund)
第2章第1节3.1 HTML document
1 markdown语言基础
- 正常段落(paragraph)。行顶头开始写文字(不要空格),结束直接按回车
Enter(不要留空格)。段落与段落之间留一行空白行。例如,如下代码和效果分别是:
这是第一段落。R markdown语言是一门新兴的写作语言,今天我们一起来学习。
这是第二段落。这是第一段落。R markdown语言是一门新兴的写作语言,今天我们一起来学习。
这是第二段落。
- 粗体(bold)、下标(subscript)和上标(upscript)。粗体以一对双星符号包括d 形式表达(
**字符**);下标以一对波浪符号包括的形式表达(~字符~);下标以一对尖帽符号包括的形式表达(^字符^)。例如,如下代码和效果分别是:
谢益辉是一个毕业于**中国人民大学**的优秀华人。
下标水分子式H~2~O;上标平方米100m^2^。谢益辉是一个毕业于中国人民大学的优秀华人。
下标水分子式H2O;上标平方米100m2。
- 列表(list):无序列表和有序列表。例如,如下代码和效果分别是:
无序列表形式1:
- 这是第一小点
- 这是第二小点
无序列表形式:
这是第一小点
这是第二小点
有序列表形式:
1. 这是第1小点
2. 这是第2小点。
- 这是2.1
- 这是2.2。
有序列表形式:
这是第1小点
这是第2小点。
这是2.1
这是2.2。
2 公式的编写技巧
- 行内公式(inline equation)。采用一对美元符号内写Latex的形式(
$LaTex$),其代码和效果如下:
行内公式就是在一行正常文字内插入公式,比如线性回归模型$Y_t =\beta_1 + \beta_2X_t + u_t$。行内公式就是在一行正常文字内插入公式,比如线性回归模型\(Y_t =\beta_1 + \beta_2X_t + u_t\)。
- 独立公式(LaTex equation)。采用一对双美元符号内写Latex公式的形式(
$LaTex equation$),其代码和效果如下:
下面将展示一个独立公式的写法:
$$\begin{align}
Y_i &= \beta_1 +\beta_2X_i +u_i \\
u_i &\sim N(0, \sigma^2)
\end{align}$$下面将展示一个独立公式的写法:
\[\begin{align} Y_i &= \beta_1 +\beta_2X_i +u_i \\ u_i &\sim N(0, \sigma^2) \end{align}\]
启示,公式编写,我们使用的是LaTex语言。所以你们要了解基本的Latex知识。还有你们需要希腊字母体系,以及统计和计量的基本知识。
3 利用R 进行数据分析和制图
简单的编码示例:
x <- 1:100
y <- c("hhp", "lisi")
x## [1] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
## [18] 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
## [35] 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51
## [52] 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68
## [69] 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85
## [86] 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100y## [1] "hhp" "lisi"数据处理过程:
# prepare pkgs
#install.packages("tidyverse")
require("tidyverse")
#install.packages("xlsx")
require("xlsx")
# read .xlsx file
data_longley <- read.xlsx("data/Table-10-8-longley.xlsx", sheetIndex = 1)
data_new <- data_longley %>%
mutate(log.Y =log(Y),
real.GDP = X3/X2)表格形式1(普通表):
require("knitr")
require("kableExtra")
data_new %>%
kable(booktab=T,caption = "这是一张傻傻的数据表") %>%
kable_styling(full_width = T)| obs | Year | Y | X2 | X3 | X4 | X5 | X6 | X7 | log.Y | real.GDP |
|---|---|---|---|---|---|---|---|---|---|---|
| 1947 | 1947 | 60323 | 830 | 234289 | 2356 | 1590 | 107608 | 1 | 11.00747 | 282.2759 |
| 1948 | 1948 | 61122 | 885 | 259426 | 2325 | 1456 | 108632 | 2 | 11.02063 | 293.1367 |
| 1949 | 1949 | 60171 | 882 | 258054 | 3682 | 1616 | 109773 | 3 | 11.00495 | 292.5782 |
| 1950 | 1950 | 61187 | 895 | 284599 | 3351 | 1650 | 110929 | 4 | 11.02169 | 317.9877 |
| 1951 | 1951 | 63221 | 962 | 328975 | 2099 | 3099 | 112075 | 5 | 11.05439 | 341.9699 |
| 1952 | 1952 | 63639 | 981 | 346999 | 1932 | 3594 | 113270 | 6 | 11.06098 | 353.7197 |
| 1953 | 1953 | 64989 | 990 | 365385 | 1870 | 3547 | 115094 | 7 | 11.08197 | 369.0758 |
| 1954 | 1954 | 63761 | 1000 | 363112 | 3578 | 3350 | 116219 | 8 | 11.06290 | 363.1120 |
| 1955 | 1955 | 66019 | 1012 | 397469 | 2904 | 3048 | 117388 | 9 | 11.09770 | 392.7559 |
| 1956 | 1956 | 67857 | 1046 | 419180 | 2822 | 2857 | 118734 | 10 | 11.12516 | 400.7457 |
| 1957 | 1957 | 68169 | 1084 | 442769 | 2936 | 2798 | 120445 | 11 | 11.12975 | 408.4585 |
| 1958 | 1958 | 66513 | 1108 | 444546 | 4681 | 2637 | 121950 | 12 | 11.10515 | 401.2148 |
| 1959 | 1959 | 68655 | 1126 | 482704 | 3813 | 2552 | 123366 | 13 | 11.13685 | 428.6892 |
| 1960 | 1960 | 69564 | 1142 | 502601 | 3931 | 2514 | 125368 | 14 | 11.15000 | 440.1060 |
| 1961 | 1961 | 69331 | 1157 | 518173 | 4806 | 2572 | 127852 | 15 | 11.14665 | 447.8591 |
| NA | 1962 | 70551 | 1169 | 554894 | 4007 | 2827 | 130081 | 16 | 11.16409 | 474.6741 |
表格形式2(交互表):
require("DT")
data_new %>%
datatable(caption = "这是一个比较有意思的交互表",
options = list(
pageLength= 5,
dom="tip"
)) %>%
formatRound(c(10:11), digits=2)图3.1: 这是一个比较有意思的交互表
下面我们来制作一幅散点图:
require("ggplot2")
data_new %>%
as_tibble() %>%
mutate(Year=as.factor(Year)) %>%
ggplot(aes(Year, real.GDP)) +
geom_point(color="blue", size=3) +
labs(x="年份(Year)", y= "实际GDP(real.GDP)") 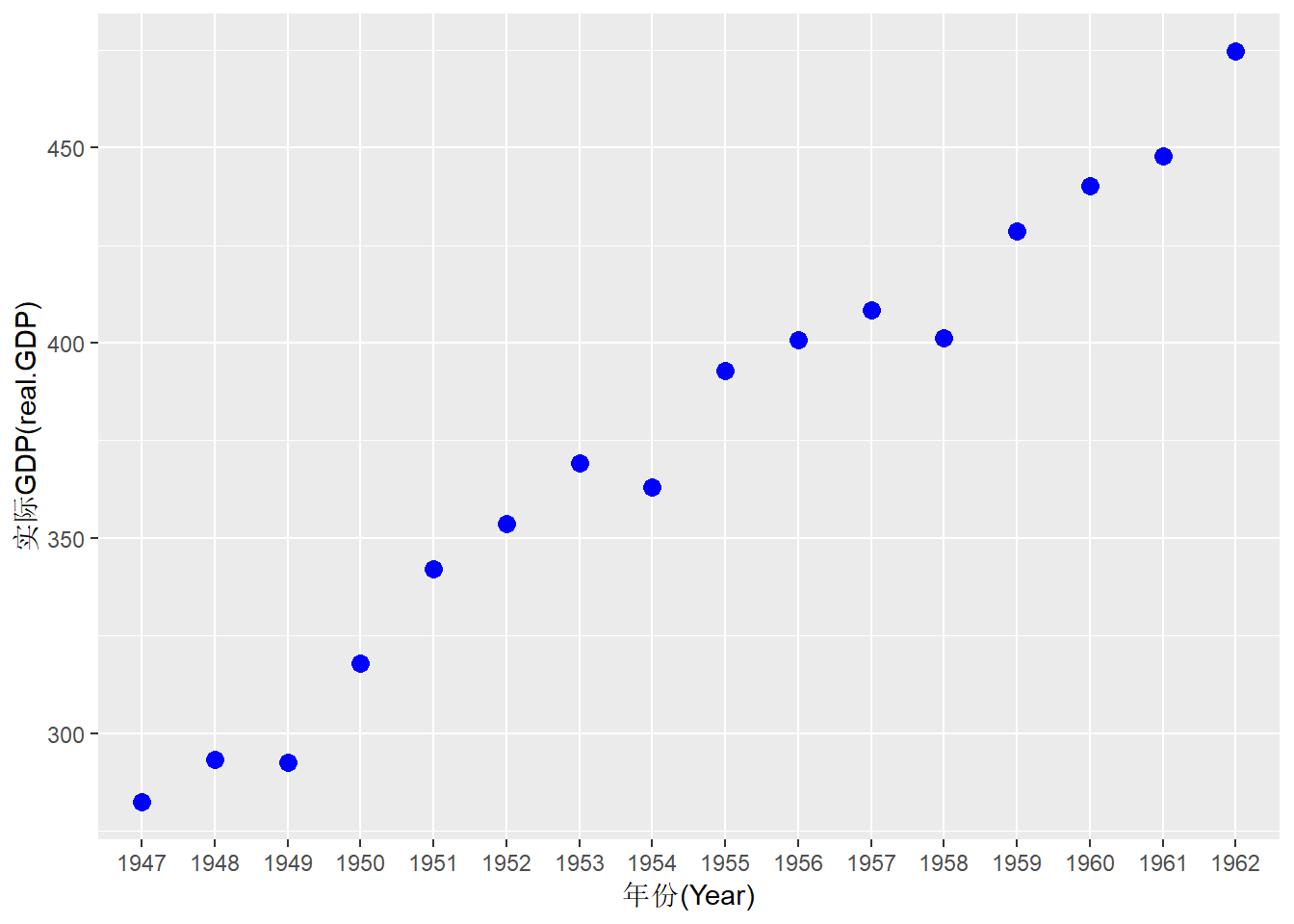
图3.2: 这是一幅傻傻的散点图