中级计量经济学
(硕士研究生2018年秋)测试题
第一部分:鳕鱼供需案例分析计算(共3大题,共75分) 得分:_______分
案例背景介绍:研究者收集了纽约市Fulton海鲜市场1991-12-02日到1992-05-08日期间共111天的相关日度数据。研究者主要关注鳕鱼产品的市场价格和数量,以及其他市场相关变量,如工作日(周一~周五)、气候条件、鳕鱼存货量变化情况等。具体变量及含义见下表:
| 变量 | 含义 | 备注 |
|---|---|---|
| price | 鳕鱼市场价格(美元/千克) | 连续变量 |
| quan | 鳕鱼的数量(吨) | 连续变量 |
| lprice | (自然)对数化的鳕鱼市场价格 | 连续变量 |
| lquan | (自然)对数化的鳕鱼数量 | 连续变量 |
| mon | 周一 | 虚拟变量:1=周一; 0=其他 |
| tue | 周二 | 虚拟变量:1=周二; 0=其他 |
| wen | 周三 | 虚拟变量:1=周三; 0=其他 |
| thu | 周四 | 虚拟变量:1=周四; 0=其他 |
| stormy | 暴风雨天气 | 虚拟变量:1=暴风雨; 0=其他 |
| cold | 寒冷天气 | 虚拟变量:1=寒冷; 0=其他 |
| change | 鳕鱼存货变化情况 | 虚拟变量:1=变化大; 0=变化小 |
请根据以上案例背景和数据,分析计算并回答下面一系列问题:
- (共计30分,共6小题)A同学重点考察鳕鱼价格的影响因素,并构建如下的多元回归价格模型:
\[\begin{align} \begin{split} lprice_t &= \beta_1+\beta_2lquan_t+\beta_3mon_t+\beta_4tue_t+\beta_5wed_t+\beta_6thu_t\\ &+\beta_7stormy_t + \beta_8cold_t + \beta_9change_t + u_{t} \end{split} \text{(价格模型)} \end{align}\]
A同学利用统计软件对上述价格模型进行OLS回归分析,得到如下报告摘要:
Call:
lm(formula = mod_mult, data = fultonfish)
Residuals:
Min 1Q Median 3Q Max
-0.835 -0.240 0.027 0.252 0.726
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.6504 0.4408 1.48 0.14321
lquan -0.0978 0.0501 -1.95 0.05343 .
mon -0.0830 0.1042 -0.80 0.42780
tue -0.0836 0.1048 -0.80 0.42677
wed -0.0732 0.1077 -0.68 0.49801
thu 0.0538 0.1008 0.53 0.59441
stormy 0.2937 0.0815 3.60 0.00049 ***
cold 0.0861 0.0713 1.21 0.22986
change -0.1478 0.0738 -2.00 0.04801 *
---
Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.341 on 102 degrees of freedom
Multiple R-squared: 0.261, Adjusted R-squared: 0.203
F-statistic: 4.5 on 8 and 102 DF, p-value: 0.000104请根据以上回归结果,回答如下问题:
(1)(5分)根据A同学的回归分析报告,请你写出相应的样本回归模型(要求写出理论表达式和数值表达式)。
(2)(2分)关于变量\(lquan\)的回归系数,它有什么样的经济学含义(请进行简单的经济学解释)?其符号和大小是否符合理论上的预期(请简要说明理由)?
(3)(5分)A同学的统计分析报告中:回归系数的t检验结果为显著(给定\(\alpha=0.1\))的变量包括哪些?(请简要说明判断依据)?回归方程的整体显著性F检验结果如何?(请简要说明判断依据)?回归方程的判定系数\(R^2\)和调整判定系数\(\bar{R}^2\)分别是多少?
(4)(5分)如果A同学给出一些已知条件{ 暴风雨;寒冷;鳕鱼存量变化小;鳕鱼的市场数量为54.5996 吨 },也即{ \(stormy=1; cold=1; change=0; quan=\) 54.5996 }。请计算在给定条件下,Fulton生鲜市场在星期五的鳕鱼期望价格是多少?(要求:请写出理论表达式,并计算出数值结果;对数计算请以自然数\(e=2.7183\)为底;计算结果保留2位小数)。
(5)(5分)为了诊断价格模型是否存在多重共线性问题,A同学利用统计软件得到了下面表2所示的方差膨胀因子计算表。
| X | lquan | mon | tue | wed | thu | stormy | cold | change |
| VIF | 1.305 | 1.592 | 1.723 | 1.697 | 1.594 | 1.302 | 1.212 | 1.106 |
根据表2的信息,请判断回归方程是否存在多重共线性问题?(请简要说明判断依据。)
(6)(小计8分,共2小问)为了诊断价格模型是否存在异方差问题,A同学利用统计软件对上述回归方程的残差\(e_t\)进行绘图,得到如下时序图(见图1):
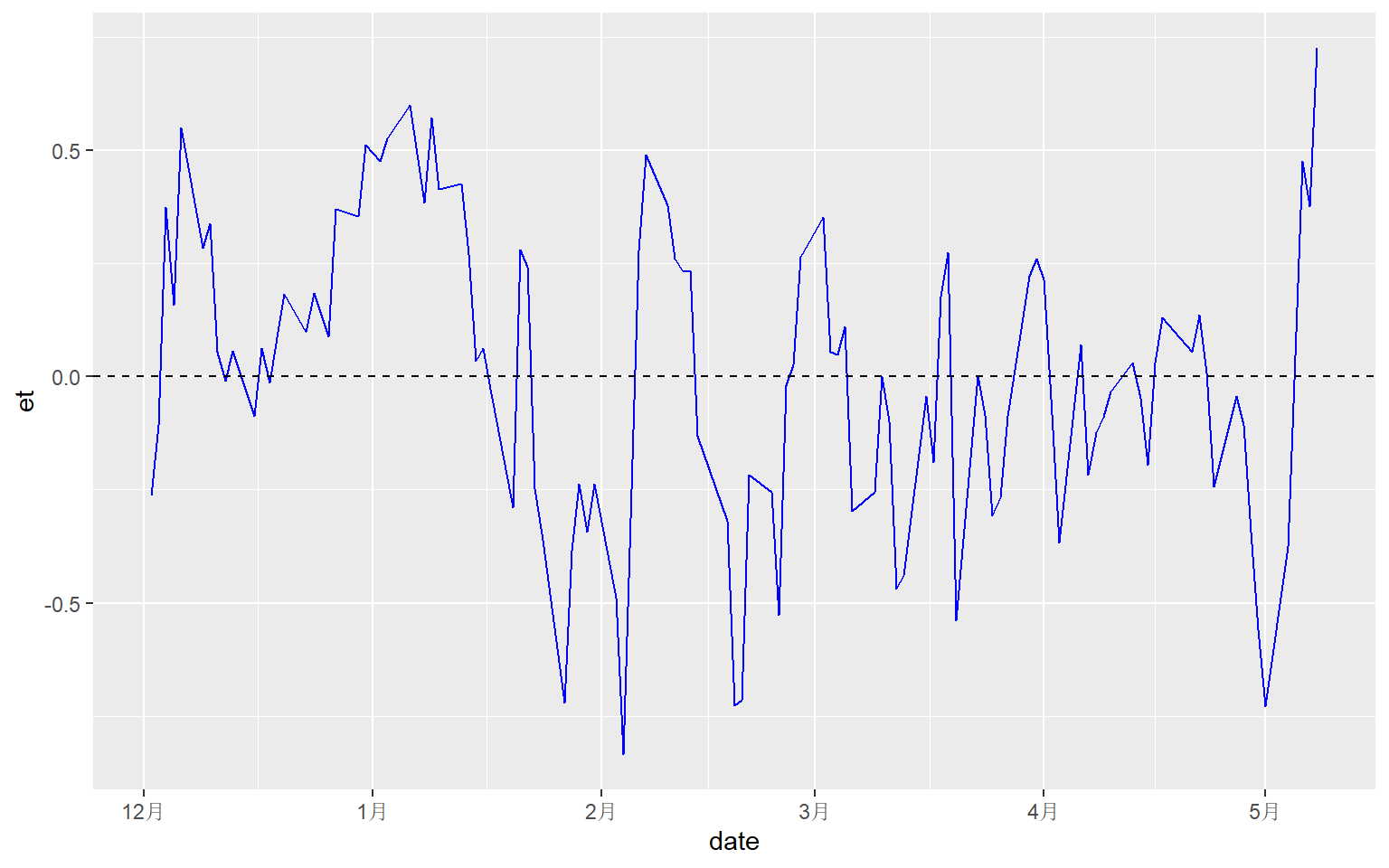
图1: 残差et的时序图
同时,为定量化地考察价格模型是否存在异方差问题。A同学决定进行怀特异方差诊断(White Test),对残差\(e_t\)构建如下辅助回归模型:
\[\begin{equation} \begin{alignedat}{999} &e_t^2=&& + \alpha_{1} && + \alpha_{2} lquan&& + \alpha_{3} mon&& + \alpha_{4} tue\\ & && + \alpha_{5} wed&& + \alpha_{6} thu&& + \alpha_{7} stormy&& + \alpha_{8} cold\\ & && + \alpha_{9} change&& + \alpha_{10} (lquan)^2&&+v_t\\ \end{alignedat} \end{equation}\]
并得到辅助回归模型的分析结果为:
\[\begin{equation} \begin{alignedat}{999} &\hat{e}_t^2=&&-1.09&&+0.30lquan&&-0.03mon&&-0.05tue\\ &\text{(t)}&&(-0.8705)&&(0.9923)&&(-0.7829)&&(-1.0942)\\ &\text{(se)}&&(1.2536)&&(0.3054)&&(0.0441)&&(0.0438)\\ &\text{(cont.)}&&-0.07wed&&-0.05thu&&+0.02stormy&&-0.00cold\\ &\text{(t)}&&(-1.4756)&&(-1.0744)&&(0.7264)&&(-0.0555)\\ &\text{(se)}&&(0.0450)&&(0.0421)&&(0.0342)&&(0.0298)\\ &\text{(cont.)}&&+0.00change&&-0.02(lquan)^2\\ &\text{(t)}&&(0.1213)&&(-1.0006)\\ &\text{(se)}&&(0.0310)&&(0.0185)\\ &\text{(fitness)}&& n=111;&& R^2=0.0429;&& \bar{R^2}=-0.0424\\ & && F^{\ast}=0.50;&& p=0.8691\\ \end{alignedat} \end{equation}\]
请根据以上分析结果,对价格模型是否存在异方差问题进行如下回答:
a)(3分)观测残差的时序图(图1),请初步判断价格模型是否存在明显的异方差问题?(请简要说明理由)。
b)(5分)利用上述怀特异方差检验的辅助回归模型的回归结果,对异方差问题进行\(\chi^2\)显著性检验。(给定\(\alpha=0.05\)水平下,理论查表值有\(\chi^2_{0.95}(9)=\) 16.92;\(\chi^2_{0.95}(10)=\) 18.31。)(要求:写出原假设\(H_0\)和备择假设\(H_1\);计算出卡方统计量\({\chi^{\ast}}^2= n\cdot R^2 \sim \chi^2(f)\);确定正确的理论查表值\(\chi^2_{1-\alpha}(f)\);明确给出价格模型是否存在异方差的诊断结论。)
- (共计20分,共3小题)B同学重点关注鳕鱼对数化价格变量\(lprice_t\)的平稳性和预测问题。
(1)(5分)为了分析对数化价格变量\(lprice_t\)的平稳性问题,B同学采用增广迪基-富勒检验法(Augmented Dickey-Fuller Test,ADF)进行验证。B同学利用统计软件分析,得出如下表(表3)所示的分析结果:
| 项目 | 细节 |
|---|---|
| 检验方法 | Augmented Dickey-Fuller Test |
| 备择假设H1 | alternative hypothesis:stationary(平稳) |
| 检验变量 | lprice |
| 迪基-富勒统计量 | Dickey-Fuller =-4.76 |
| 滞后阶数 | Lag order =4 |
| 概率值 | p-value =0.01 |
请根据以上信息,判断对数化价格变量\(lprice_t\)是不是平稳时间序列?(请简要给出理由。)
(2)(5分)为了识别对数化价格变量\(lprice_t\)的波动模式,B同学进一步绘制出了\(lprice_t\)序列的自相关图(ACF,见图2)和偏自相关图(PACF,见图3)
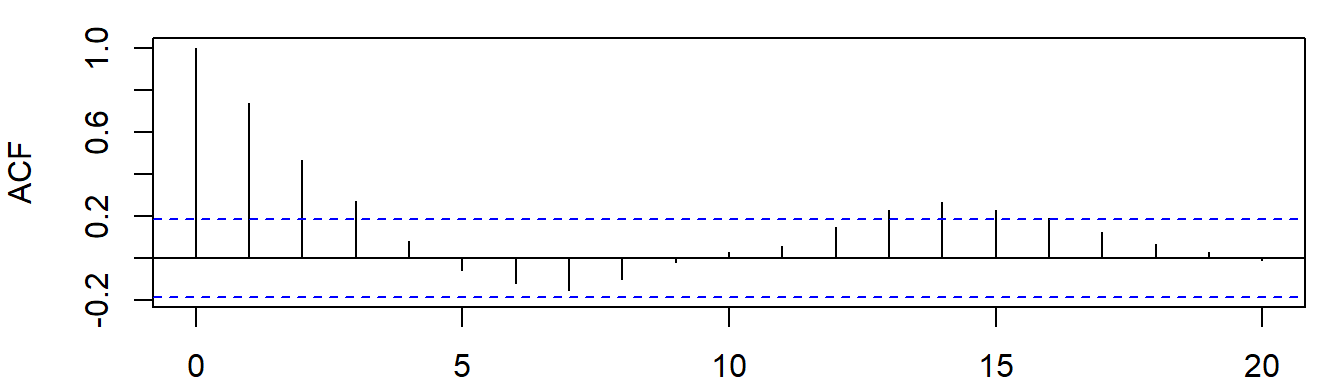
图2: 对数化价格变量lprice的自相关图
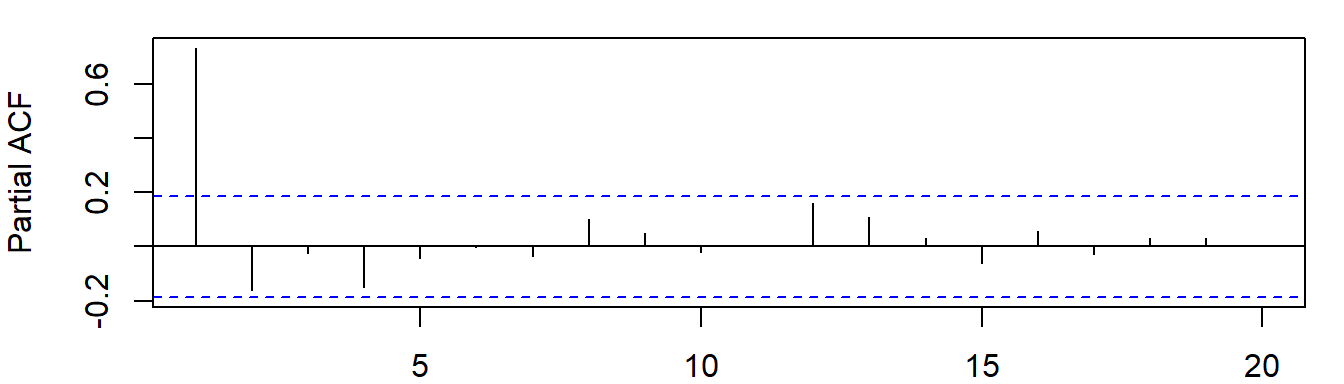
图3: 对数化价格变量lprice的偏自相关图
请根据以上图形信息,初步判断对数化价格变量\(lprice_t\)的时间序列过程是属于哪一种模式?(要求:指明是AR过程/MA过程/ARMA过程中的哪一种,不需要指明阶数,并给出简要理由。)
(3)(小计10分,共2小问)为进一步对变量\(lprice_t\)进行准确\(ARMA(p,q)\)建模,B同学尝试进行\(ARMA(2,0)\)建模分析。B同学使用统计软件,得到如下分析结果:
Series: fultonfish$lprice
ARIMA(2,0,0) with non-zero mean
Coefficients:
ar1 ar2 mean
0.908 -0.198 -0.186
s.e. 0.095 0.095 0.079
sigma^2 estimated as 0.0625: log likelihood=-2.55
AIC=13.1 AICc=13.47 BIC=23.93同时,B同学进一步对以上\(ARMA(2,0)\)建模结果的残差绘图,得到回归残差的自相关图(ACF,见图4)和偏自相关图(PACF,见图5)
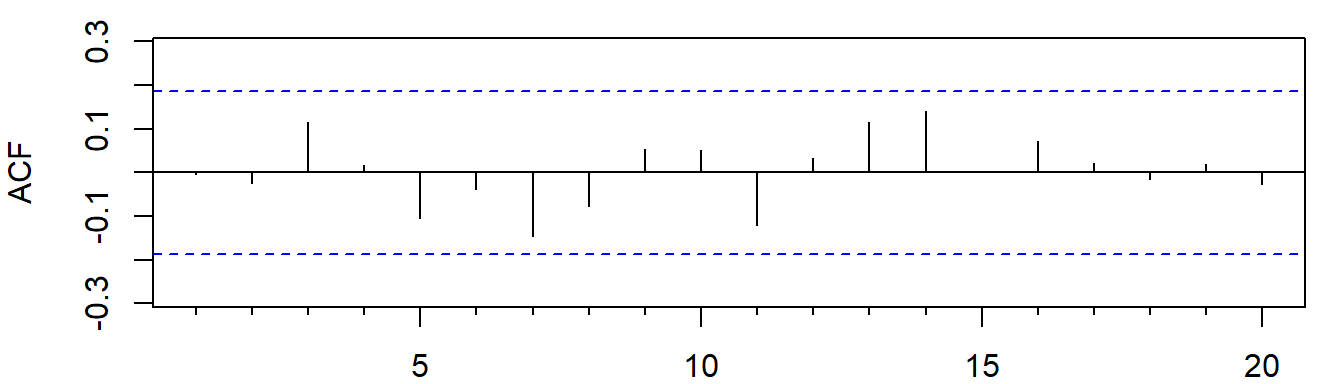
图4: 残差的自相关图
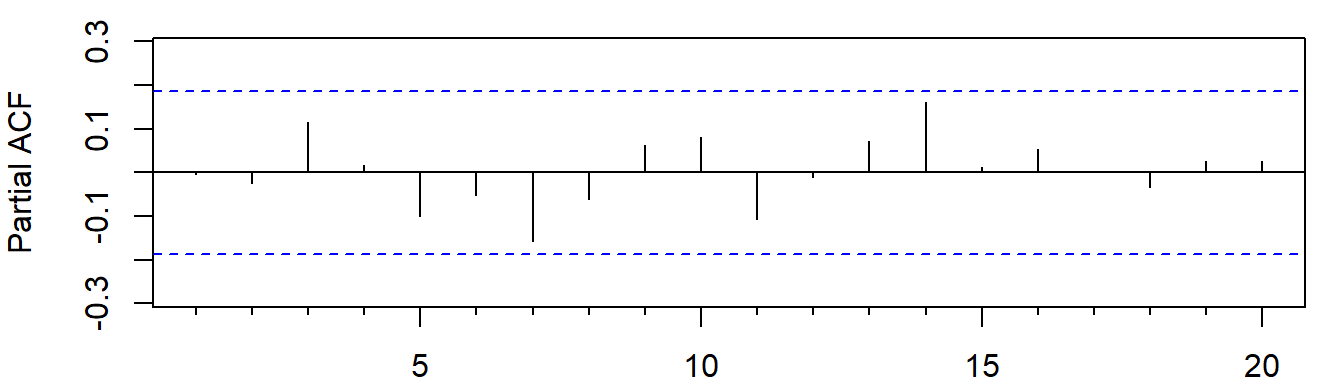
图5: 残差的偏自相关图
请回答:
a)(6分)根据分析报告摘要信息,写出\(ARMA(2,0)\)模型的样本回归方程形式。
b)(4分)根据残差绘图结果(图4和图5),判断B同学的\(ARMA(2,0)\)建模是否合理,并给出简要理由。
- (共计25分,共5小题)C同学重点关注鳕鱼供需关系的联立方程建模分析。
对此,C同学构建了如下的联立方程:
\[\begin{align} lquan_t &= \alpha_0+\alpha_1lprice_t+\alpha_2mon_t+\alpha_3tue_t+\alpha_4wen_t+\alpha_5thu_t+u_{1,t} &\text{(需求方程)} \\ lquan_t &= \beta_0+\beta_1lprice_t+\beta_3stormy_t+u_{2,t} &\text{(供给方程)} \end{align}\]
(1)(3分)对于以上联立方程模型,需求方程中变量\(lprice_t\)的参数\(\alpha_1\),以及供给方程中变量\(lprice_t\)的参数\(\beta_1\),理论上这两个参数的大小和符号应该分别有什么要求?
(2)(5分)请根据阶条件规则,对上述联立方程模型中需求方程和供给方程分别作出识别性问题的判断,并请说明判断依据。
(3)(5分)请将以上需求方程和供给方程分别表达成约简方程形式。(要求:不需要写出结构系数与约简系数的关系式。数量方程(\(lquan\))约简系数记为\(\pi_{1,p} \ \ (p=1,2,...)\),随机干扰项记为\(v_{1,t}\);价格方程(\(lprice\))约简系数记为\(\pi_{2,q} \ \ (q=1,2,...)\),随机干扰项记为\(v_{2,t}\)。)
(4)(小计6分,共2小问)C同学直接使用普通最小二乘法(OLS)对前述第(3)问中的约简方程分别进行回归,并得到如下分析结果。
对数化鳕鱼数量(\(lquan\))的约简方程OLS回归结果为: \[\begin{equation} \begin{alignedat}{999} &\widehat{lquan}=&&+8.81&&+0.10mon&&-0.48tue\\ &\text{(t)}&&(59.9225)&&(0.4891)&&(-2.4097)\\ &\text{(se)}&&(0.1470)&&(0.2065)&&(0.2011)\\ &\text{(cont.)}&&-0.55wed&&+0.05thu&&-0.39stormy\\ &\text{(t)}&&(-2.6875)&&(0.2671)&&(-2.6979)\\ &\text{(se)}&&(0.2058)&&(0.2010)&&(0.1437)\\ &\text{(fitness)}&& n=111;&& R^2=0.1934;&& \bar{R^2}=0.1550\\ & && F^{\ast}=5.03;&& p=0.0004\\ \end{alignedat} \end{equation}\]
对数化鳕鱼价格(\(lprice\))的约简方程OLS回归结果为: \[\begin{equation} \begin{alignedat}{999} &\widehat{lprice}=&&-0.27&&-0.11mon&&-0.04tue\\ &\text{(t)}&&(-3.5569)&&(-1.0525)&&(-0.3937)\\ &\text{(se)}&&(0.0764)&&(0.1073)&&(0.1045)\\ &\text{(cont.)}&&-0.01wed&&+0.05thu&&+0.35stormy\\ &\text{(t)}&&(-0.1106)&&(0.4753)&&(4.6387)\\ &\text{(se)}&&(0.1069)&&(0.1045)&&(0.0747)\\ &\text{(fitness)}&& n=111;&& R^2=0.1789;&& \bar{R^2}=0.1398\\ & && F^{\ast}=4.58;&& p=0.0008\\ \end{alignedat} \end{equation}\]
a)(4分)如果已知条件为{ 周一;暴风雨 },也即{ \(mon=1; stormy=1\) }。在给定条件下,根据上述约简方程结果,请计算Fulton生鲜市场的鳕鱼价格 \(price\) 和鳕鱼数量 \(quan\)分别是多少?(要求:对数计算请以自然数 \(e=2.7183\) 为底;计算结果保留2位小数)。
b)(2分)C同学坚持认为:以上步骤计算得到的鳕鱼价格\(price\)和鳕鱼数量\(quan\)就是Fulton生鲜市场在周一且天气为暴风雨时的市场均衡价格和市场均衡数量。你认为C同学的观点是否正确?请简要说明你的理由。
(5)(小计6分,共2小问)C同学随后又采用了两阶段最小二乘法(2SLS)对联立方程模型进行了回归分析,得到如下表所示的分析结果(见表4):
| eq | vars | Estimate | Std. Error | t value | Pr(>|t|) |
|---|---|---|---|---|---|
| eq1 | (Intercept) | 8.5059 | 0.1662 | 51.1890 | 0.0000 |
| eq1 | lprice | -1.1194 | 0.4286 | -2.6115 | 0.0103 |
| eq1 | mon | -0.0254 | 0.2148 | -0.1183 | 0.9061 |
| eq1 | tue | -0.5308 | 0.2080 | -2.5518 | 0.0122 |
| eq1 | wed | -0.5664 | 0.2128 | -2.6620 | 0.0090 |
| eq1 | thu | 0.1093 | 0.2088 | 0.5233 | 0.6018 |
| eq2 | (Intercept) | 8.6284 | 0.3890 | 22.1826 | 0.0000 |
| eq2 | lprice | 0.0011 | 1.3095 | 0.0008 | 0.9994 |
| eq2 | stormy | -0.3632 | 0.4649 | -0.7813 | 0.4363 |
a)(2分)基于以上分析报告,请你计算出鳕鱼的需求价格弹性\(\eta_1\)和供给价格弹性\(\eta_2\)分别是多少?
b)(4分)基于以上分析报告,请你帮C同学计算出Fulton生鲜市场在周一且天气为暴风雨时(也即{ mon=1; stormy=1 })鳕鱼的市场均衡价格和市场均衡数量。(计算结果保留2位小数。)
第二部分:乳腺癌案例分析计算 (共5小题,共25分) 得分:_______分
案例背景介绍:一项关于女性乳腺癌患病情况的控制性研究,收集了共178名女性的相关资料。研究者主要关注二分类变量是否患乳腺癌(\(Cancer\)),以及与其他相关变量的关系,如年龄、受教育年数、是否接受过正规检查、生育第一胎时的年龄、流产次数、体重等。具体变量及含义见下表所示(5)
| 变量 | 含义 | 备注 |
|---|---|---|
| Cancer | 是否患乳腺癌 | 虚拟变量:1=患有乳腺癌; 0=未患乳腺癌 |
| Age | 年龄(岁) | 数值变量 |
| HIGD | 受教育年数(年) | 数值变量 |
| CHK | 是否接受过正规检查 | 虚拟变量:1=接受过正规检查; 0=未接受过正规检查 |
| AGPI | 生育第一胎时的年龄 | 数值变量 |
| Miscar | 流产次数(次) | 数值变量 |
| Births | 生育子女数(个) | 数值变量 |
| Weight | 体重(磅) | 数值变量 |
对变量是否患有乳腺癌\((Cancer)\),构造如下的总体回归模型(见公式(1)):
\[\begin{equation} \begin{alignedat}{999} &Cancer=&& + \beta_{1} && + \beta_{2} Age&& + \beta_{3} HIGD\\ &\text{(cont.)}&& + \beta_{4} CHK&& + \beta_{5} AGPI&& + \beta_{6} Miscar\\ &\text{(cont.)}&& + \beta_{7} Births&& + \beta_{8} Weight&&+u\\ \end{alignedat} \tag{1} \end{equation}\]
研究者对上述模型(公式(1))进行logit形式的极大似然估计,统计软件的分析结果如下表所示(见表6):
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | -0.5273 | 2.3190 | -0.2274 | 0.8201 |
| Age | 0.0058 | 0.0219 | 0.2660 | 0.7902 |
| HIGD | -0.0615 | 0.0860 | -0.7144 | 0.4750 |
| CHK | -1.5960 | 0.5286 | -3.0191 | 0.0025 |
| AGPI | 0.1339 | 0.0562 | 2.3844 | 0.0171 |
| Miscar | 0.3415 | 0.2395 | 1.4257 | 0.1540 |
| Births | 0.2923 | 0.1302 | 2.2455 | 0.0247 |
| Weight | -0.0294 | 0.0100 | -2.9310 | 0.0034 |
基于以上的logit回归分析,研究者统计了乳腺癌患病预测情况,具体见下面的表7:
| 真实值 | 预测值 | 频次 |
|---|---|---|
| 0 | 0 | 130 |
| 1 | 0 | 28 |
| 0 | 1 | 8 |
| 1 | 1 | 12 |
请回答下面的一系列问题:
(1)(5分)给定\(Y_i\)为二分类变量,\(X_i\)为连续变量,如果分别构建probit模型和logit模型,并令概率\(P(Y_i=1|X) = \Phi(\beta_0+\beta_1X_i)\),且令\(Z_i=\beta_0+\beta_1X_i\)。研究人员分别绘制下图所示的累积概率曲线(见图6)。
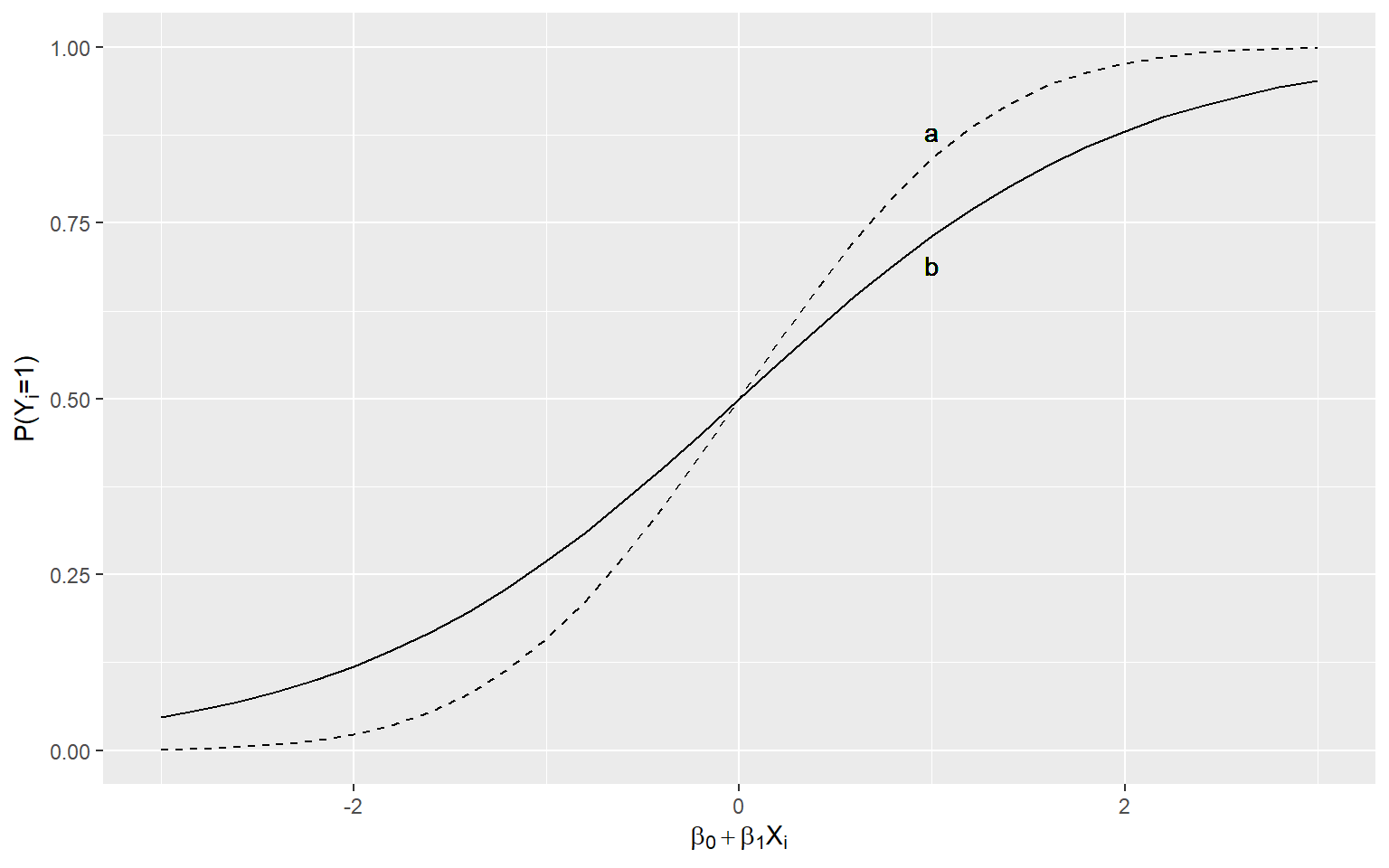
图6: probit模型和logit模型下的累积概率曲线
请指出图6中,probit累积概率曲线和logit累积概率密度曲线分别是哪一条?并请写出logit累积概率函数表达式。
(2)(5分)根据Logit回归估计结果(见表6),请正确写出logit样本回归函数。(要求:logit变量用\(L_i\)表达;回归系数保留4位小数)。
(3) (5分)根据logit回归的预测情况统计(见表7),请计算拟合优度指标——计数\(R^2\)值。(要求:写出理论计算公式;计算结果保留2位小数)
(4)(5分)如果已经计算得到似然比统计量 \(LR^{\ast}= {\chi^2}^{\ast}=\) 25.97,请对logit回归进行模型整体显著性卡方检验。(给定\(\alpha=0.05\)水平下,卡方分布的理论查表值有\(\chi^2_{0.95}(7)=\) 14.07;\(\chi^2_{0.95}(8)=\) 15.51。)(要求:写出原假设\(H_0\)和备择假设\(H_1\);确定正确的理论查表值\(\chi^2_{1-\alpha}(f)\);明确给出模型整体显著性检验结论。)
(5)(5分)根据logit回归结果,请计算一个接受过正规检查(也即\(CHK=1\))与一个未接受过正规检查(也即\(CHK=0\))的女性,两种情形下罹患乳腺癌的机会比率值是多少(假定其他条件不变)?
参考答案
第一部分:鳕鱼供需案例分析计算(共3大题,共75分)
- 答:
(1)答:
理论表达式为:
\[\begin{equation} \begin{alignedat}{999} &\widehat{lprice}=&&+\hat{\beta}_{1}&&+\hat{\beta}_{2}lquan&&+\hat{\beta}_{3}mon&&+\hat{\beta}_{4}tue\\ &\text{(cont.)}&&+\hat{\beta}_{5}wed&&+\hat{\beta}_{6}thu&&+\hat{\beta}_{7}stormy&&+\hat{\beta}_{8}cold\\ &\text{(cont.)}&&+\hat{\beta}_{9}change\\ \end{alignedat} \end{equation}\]
数值表达式为:
\[\begin{equation} \begin{alignedat}{999} &\widehat{lprice}=&&+0.65&&-0.10lquan&&-0.08mon&&-0.08tue\\ &\text{(t)}&&(1.4753)&&(-1.9541)&&(-0.7961)&&(-0.7979)\\ &\text{(se)}&&(0.4408)&&(0.0501)&&(0.1042)&&(0.1048)\\ &\text{(cont.)}&&-0.07wed&&+0.05thu&&+0.29stormy&&+0.09cold\\ &\text{(t)}&&(-0.6801)&&(0.5341)&&(3.6030)&&(1.2080)\\ &\text{(se)}&&(0.1077)&&(0.1008)&&(0.0815)&&(0.0713)\\ &\text{(cont.)}&&-0.15change\\ &\text{(t)}&&(-2.0013)\\ &\text{(se)}&&(0.0738)\\ &\text{(fitness)}&& n=111;&& R^2=0.2610;&& \bar{R^2}=0.2030\\ & && F^{\ast}=4.50;&& p=0.0001\\ \end{alignedat} \end{equation}\]
(2)答:变量\(lquan\)的回归系数\(\hat{\beta}_2\)表示价格对数量的弹性,\(\hat{\beta}_2=-0.0978\),表示数量每增加它有什么样的经济学1%,价格会降低0.0978%。因为此处不能确定模型是否为需求函数还是供给函数,所以无法对起理论上的取值做出预期判断。
(3)答:在\(\alpha=0.1\)水平下,通过观察pr(>|t|)一列可以发现t检验结果显著的回归元有3个:\(lquan;stormy; change\)。F检验的\(F^{\ast}=4.5\),其对应的p概率值远远小于0.01,表明F检验结果为极显著。回归方程的判定系数\(R^2=0.261\),调整判定系数\(\bar{R}^2=0.203\)。
(4)答:{ \(mon=0; tue=0; wed=0; thu=0; stormy=1; cold=1; change=0; quan=\) 54.5996 }情形下的期望价格计算公式为:
\[\begin{align} \begin{split} E(lprice&|lquan=4;mon=0;tue=0;wed=0;thu=0;stormy=1;cold=1;change=0)\\ =&+\beta_{1}+\beta_{2}(4)+\beta_{3}(0)+\beta_{4}(0)+\beta_{5}(0)\\ &+\beta_{6}(0)+\beta_{7}(1)+\beta_{8}(1)+\beta_{9}(0)\\ =&+\beta_{1}+4\beta_{2}\\ &+\beta_{7}+\beta_{8}\\ \end{split} \end{align}\]
具体数值计算结果为:
\[\begin{align} \begin{split} (\widehat{lprice}&|lquan=4;mon=0;tue=0;wed=0;thu=0;stormy=1;cold=1;change=0)\\ =&+\hat{\beta}_{1}+\hat{\beta}_{2}(4)+\hat{\beta}_{3}(0)+\hat{\beta}_{4}(0)+\hat{\beta}_{5}(0)\\ &+\hat{\beta}_{6}(0)+\hat{\beta}_{7}(1)+\hat{\beta}_{8}(1)+\hat{\beta}_{9}(0)\\ =&+[0.65]+[-0.10]\cdot(4)+[-0.08]\cdot(0)+[-0.08]\cdot(0)+[-0.07]\cdot(0)\\ &+[0.05]\cdot(0)+[0.29]\cdot(1)+[0.09]\cdot(1)+[-0.15]\cdot(0)\\ =&0.6388\\ \end{split} \end{align}\]
因此,可以计算得出Fulton生鲜市场在星期五的鳕鱼期望价格是\(price=e^{0.6388}=\) 1.8942 美元/KG
(5)答:不存在多重共线性问题。因为每个变量的VIF都小于10。
(6)答:
a)初步认为存在异方差问题。因为从残差图表现出均值波动的特征。
b)
第一步,提出假设:\(H_0:\)同方差性;\(H_1:\)异方差性。
第二步,计算样本统计量:\(\chi^{\ast} = n \cdot R^2=111*0.0429=\) 4.7619
第三步,与查表值比较:\(\chi^{\ast} =\) 4.7619 \(< \chi_{0.95}(9)=\) 16.92
第四步,得出结论:在\(\alpha =0.05\)水平下,不能显著拒绝原假设\(H_0\),应接受\(H_0\),认为模型是同方差性的。
(1)答:ADF检验结果的概率值\(p=0.01\),表明显著拒绝原假设\(H_0\)(非平稳性),从而接受备择假设\(H_1\),认为序列\(lprice_t\)是平稳的。
(2)答:ACF图形为波动模式,PACF图形为截尾模式,初步判断为序列\(lprice_t\)是AR过程。
(3)
a) 答:根据摘要报告信息,可以将ARMA(2, 0)模型的样本回归方程整理为:
\[ \begin{align} \widehat{lprice}_t = -0.186 +0.908 lprice_{t-1} -1.98lprice_{t-2} \end{align} \]
a) 答:初步认为ARMA(2, 0)建模是合理的。因为模型残差的ACF和PACF图表明残差是平稳的且没有显著的波动模式。
- 答:
(1)答:理论上,需求方程中的\(\alpha_1\)表示需求的价格弹性,因此\(-1 < \alpha_1 < 0\); 同理供给方程中的\(\beta_1\)表示需求的价格弹性,因此\(0 < \beta_1 < 1\)。
(2)答:
对于需求方程:\(K=5,k=4,m=2\),因此有\(K-k=1, m-1=1\),也即\((K-k)=(m-1)\),阶条件法则表明需求方程是恰好识别;
对于供给方程:\(K=5,k=1,m=2\),因此有\(K-k=5, m-1=1\),也即\((K-k)>(m-1)\),阶条件法则表明供给方程是过度识别;
(3)答:以上结构方程组可以转换为如下的约简方程组: \[ \begin{alignat}{3} lquan_t &&= \Pi_{1,0} + \Pi_{1,1}mon_t+\Pi_{1,2}tue_t+\Pi_{1,3}wen_t+\Pi_{1,4}thu_t\\ &&+\Pi_{1,5}stormy_t+v_{1,t} \text{(约简方程1)}\\ lprice_t &&= \Pi_{2,0} + \Pi_{2,1}mon_t+\Pi_{2,2}tue_t+\Pi_{2,3}wen_t+\Pi_{2,4}thu_t\\ &&+\Pi_{2,5}stormy_t+v_{2,t} \text{(约简方程2)}\\ \end{alignat} \]
(4)答:
a)答:
{ 周一;暴风雨 },也即{ \(mon=1; stormy=1\) }情形下:
鳕鱼价格\(price\)的计算结果为:
\[\begin{align} \begin{split} E(lprice&|mon=1;tue=0;wed=0;thu=0;stormy=1)\\ =&+\beta_{1}+\beta_{2}(1)+\beta_{3}(0)+\beta_{4}(0)+\beta_{5}(0)+\beta_{6}(1)\\ =&+\beta_{1}+\beta_{2}+\beta_{6}\\ \end{split} \end{align}\]
\[\begin{align} \begin{split} (\widehat{lprice}&|mon=1;tue=0;wed=0;thu=0;stormy=1)\\ =&+\hat{\beta}_{1}+\hat{\beta}_{2}(1)+\hat{\beta}_{3}(0)\\ &+\hat{\beta}_{4}(0)+\hat{\beta}_{5}(0)+\hat{\beta}_{6}(1)\\ =&+[-0.27]+[-0.11]\cdot(1)+[-0.04]\cdot(0)\\ &+[-0.01]\cdot(0)+[0.05]\cdot(0)+[0.35]\cdot(1)\\ =&-0.0382\\ \end{split} \end{align}\]
因此,可以计算得出Fulton生鲜市场在{ 周一;暴风雨 }的鳕鱼价格是\(price=e^{-0.0382}=\) 0.9625 美元/KG
鳕鱼数量\(quan\)的计算结果为:
\[\begin{align} \begin{split} E(lquan&|mon=1;tue=0;wed=0;thu=0;stormy=1)\\ =&+\beta_{1}+\beta_{2}(1)+\beta_{3}(0)+\beta_{4}(0)+\beta_{5}(0)+\beta_{6}(1)\\ =&+\beta_{1}+\beta_{2}+\beta_{6}\\ \end{split} \end{align}\]
\[\begin{align} \begin{split} (\widehat{lquan}&|mon=1;tue=0;wed=0;thu=0;stormy=1)\\ =&+\hat{\beta}_{1}+\hat{\beta}_{2}(1)+\hat{\beta}_{3}(0)\\ &+\hat{\beta}_{4}(0)+\hat{\beta}_{5}(0)+\hat{\beta}_{6}(1)\\ =&+[8.81]+[0.10]\cdot(1)+[-0.48]\cdot(0)\\ &+[-0.55]\cdot(0)+[0.05]\cdot(0)+[-0.39]\cdot(1)\\ =&8.5233\\ \end{split} \end{align}\]
因此,可以计算得出Fulton生鲜市场在{ 周一;暴风雨 }的鳕鱼数量是\(quan=e^{8.5233}=\) 5030.6275 吨。
b)答:C同学的观点是不正确的。因为联立方程简单地采用OLS估计,并不能判明供给方程和需求方程的真实情况,也就是说OLS方法估计的结果是不可靠的。
(5)答:
a)答:由回归分析报告易知:
需求价格弹性\(\eta_1=\hat{\alpha}_1 = -1.1194\);
供给价格弹性\(\eta_2=\hat{\beta}_1 = 0.0011\)。
b)答:{ 周一;暴风雨 },也即{ \(mon=1; stormy=1\) }情形下:
鳕鱼价格\(price\)的计算结果为:
\[\begin{align} \widehat{lquan}|(mon=1; stormy=1) & = \hat{\alpha}_0 + \hat{\alpha}_1 lprice +\hat{\alpha}_2 \\ \widehat{lquan}|(mon=1; stormy=1) & = \hat{\beta}_0 + \hat{\beta}_1 lprice +\hat{\beta}_2 \\ \widehat{lquan}|(mon=1; stormy=1) & = 8.5059 - 1.1194 lprice -0.0254 \\ \widehat{lquan}|(mon=1; stormy=1) & = 8.6284 + 0.0011 lprice -0.3632 \\ lquan|(mon=1; stormy=1) & = 8.27 \\ lprice|(mon=1; stormy=1) & = 0.19 \\ quan|(mon=1; stormy=1) & = e^{lquan} = 3904.95 \\ price|(mon=1; stormy=1) & = e^{lprice} = 1.21 \\ \end{align}\]
第二部分:乳腺癌案例分析计算 (共5小题,共25分)
(1)答:a是probit累积概率密度曲线;b是logit累积概率密度曲线。Logit累积概率函数的表达式为:
\[\begin{align} P(Z_i) & = \frac{1}{1+e^{-Z_i}} \\ Z_i & = \beta_0 + \beta_1X_{1,i} + ... + \beta_kX_{k,i} + u_i \end{align}\]
(2)答:Logistic样本回归模型为:
\[\begin{equation} \begin{alignedat}{999} &L_i=&& -0.5273 && 0.0058 Age&& -0.0615 HIGD\\ &\text{(cont.)}&& -1.5960 CHK&& +0.1339 AGPI&& + 0.3415 Miscar\\ &\text{(cont.)}&& + 0.2923 Births&& -0.0294 Weight&&+ e_i\\ \end{alignedat} \end{equation}\]
(3)计数\(R^2\)值计算结果如下:
计数\(R^2=\frac{Y_i的正确预测数}{Y_i的总观测数n}=\frac{130+12}{178}=0.7978\)
(4)答:
第一步,提出假设:\(H_0:\beta_i,i \in (2,3,...,8)\)全部等于0;\(H_1:\beta_i,i \in (2,3,...,8)\)不全为0。
第二步,计算样本统计量:\(LR^{\ast}=\chi^{\ast} = 25.97\)
第三步,与查表值比较:\(\chi^{\ast} = 25.97 > \chi_{0.95}(7)=\) 14.07
第四步,得出结论:在\(\alpha =0.05\)水平下,显著拒绝原假设\(H_0\),应接受\(H_1\),认为模型是整体显著的。
(5)答: CHK前的拟合系数为-1.5960,因此\(ln(\frac{P_i}{1-P_i})=ln(odd)=-1.5960\),进而\(odd=e^{-1.5960}=0.2027\)