实验设计

本次计量实验中，每个学生都会拿到一份来自同一个总体的独立样本数据。

其中，该总体被设定为：

\[\begin{align} Y_i = 17 + 0.6X_i +u_i, \quad u_i \sim N(0,9) \end{align}\]

也即总体参数：\(\beta_1=17,\quad \beta_2=0.6,\quad \sigma^2=9\)。

读取学生信息

下面我们会先把学生信息读取得到：

产生模拟样本数据

然后给每个学生都随机生成独立的样本数据（n=10）：

把学生实验结果进行展示

绘制每一个人的结果图

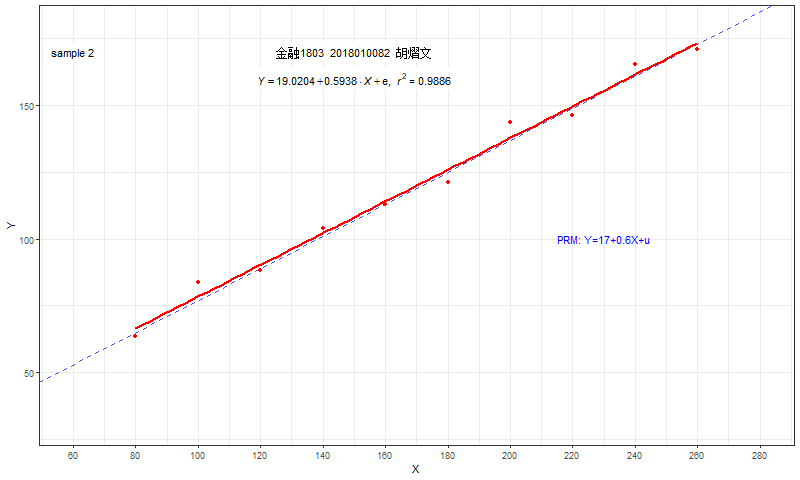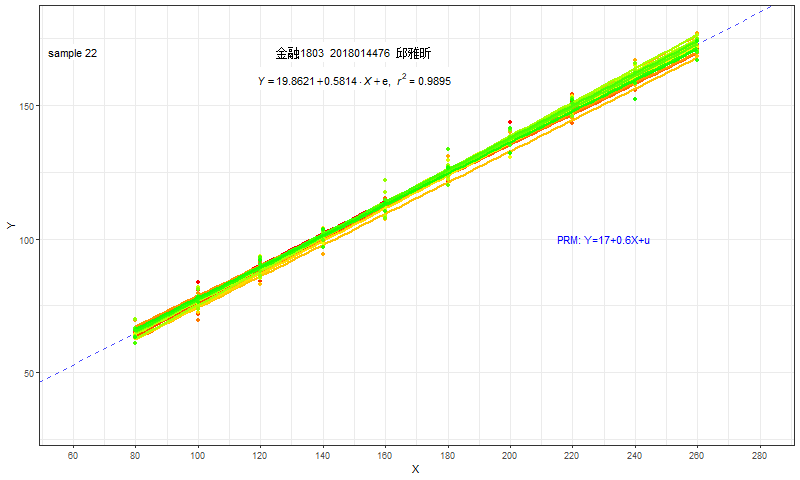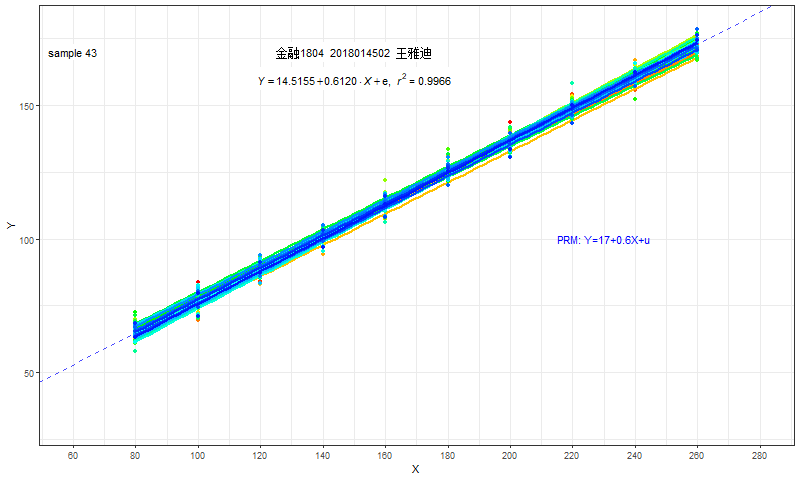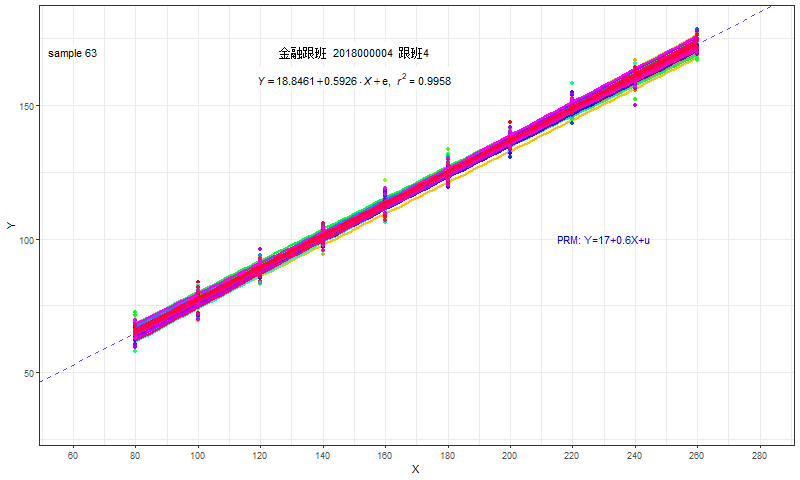
每一个同学都会利用自己的样本数据，独立地计算得到自己的OLS估计结果。

  • 每个人估计的截距系数\(\hat{\beta}_1\)和斜率系数\(\hat{\beta}_2\)都不相同
  • 每个人的结果也并不等于真实截距参数\({\beta}_1=17\)或真实斜率参数\({\beta}_2=0.6\)

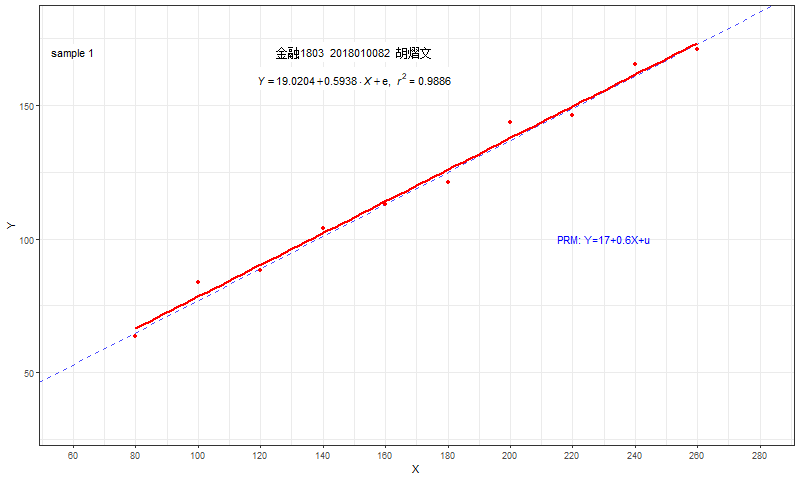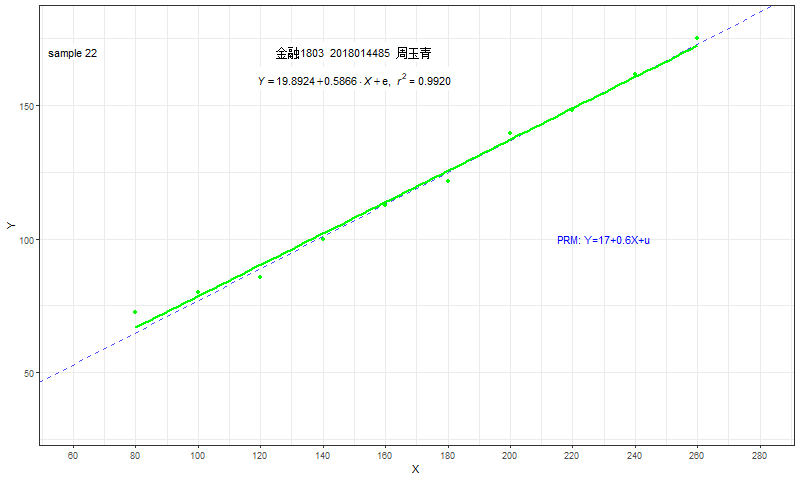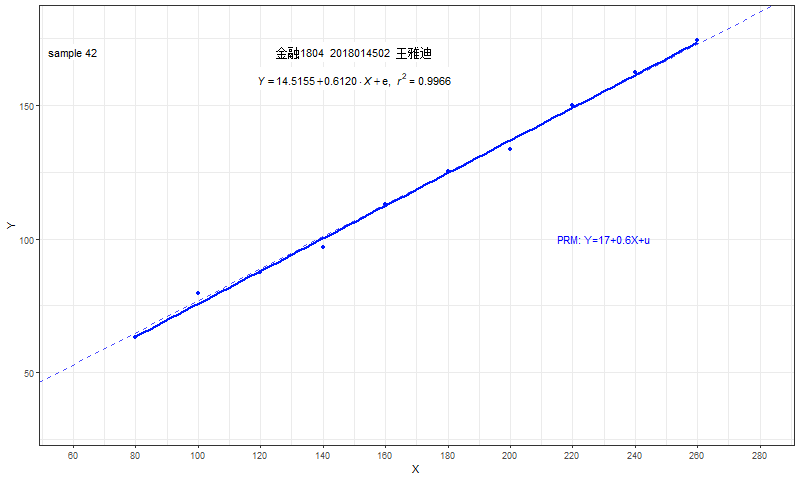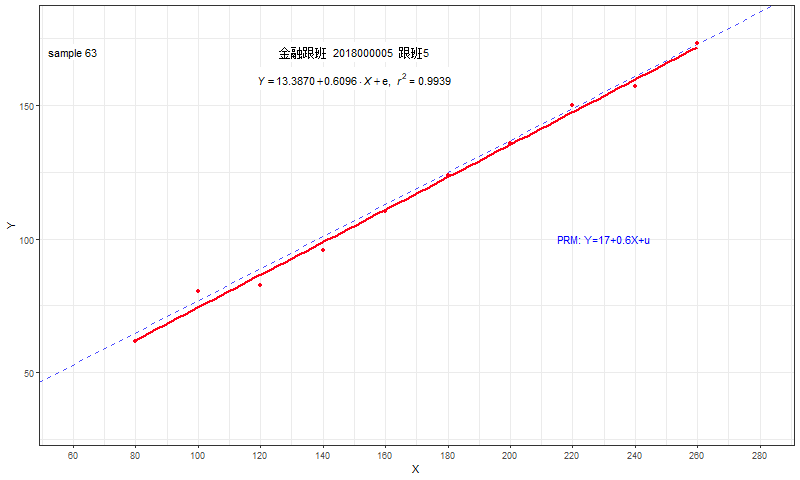
绘制所有人的结果图

我们可以把所有同学的估计结果，进行“叠加”。

  • 尽管每个同学的结果各不相同，大家也并不知道总体参数是多少。

  • 但是，全部同学的回归结果都会落在一个“范围”之内。

总结

通过这一次实验操作练习，大家可以：

  • 进一步熟悉一元回归分析的理论内容

  • 掌握一元回归分析OLS方法流程中，每一个理论步骤的软件实现

  • 理解样本回归估计量与总体参数之间的关系