风语者：计量经济学语言
孩时的方言事件
打小时起，我就对各种村落方言带来的困惑感受至深。我的故乡，属于典型的南方村落。古时是被算作南蛮之地的，外族异性零落杂居。虽然还不至于一村一俗，但是一村一个方言那是十分常见。我们村周边，3里地范围内，大概分布4个村落，就存在4种方言。好在距离不是太远，自小接触融通，还不至于听不懂。这种方言的差异，不是普通人想象的口音上的差异。就我而言，也仅限于听懂而已，要是模仿发音，那实在是难于上青天。
我的家庭里就有两种方言，母亲带来了4里远的外婆家族的方言。大姨嫁到离我家约6里地远的村子，那种村落语言对于小时候的我简直就是外星语一般的存在。因为暑假或春节会到大姨家待上一阵子，我总有一种被那个村落完全隔绝的感觉。因为无法跟这个村里其他小孩对话沟通，我大多数情况都是跟在表哥的屁股后面，生怕落单。有一次，村里一个热心的小孩看到我一个人在路边独自玩得起劲，就凑过来打招呼，可能是希望加入一起玩耍的意思。但是他的方言发音咿咿呀呀，我一个字都不懂。再加上这小孩神情诡谲，动作夸张，我飞一般地赶紧逃离是非之地，躲进大姨家里半天没出门。表哥知道后，找来那小孩问明来由，一通翻译，真相大白，大家笑得肚疼。因为这事，小孩这句接头暗话，都是目前为止我唯一能说出来而且知道意思的该村方言了，真是印象至深。
- 小孩的方言发音（此处纯粹表达出发音）:
“哟斯呗嗟嘎？哈粤郭。”
- 我当时理解的意思是：
“你是北京来的？唱个歌吧。”（我天生五音不全！）
- 表哥翻译的结果是：
“你是哪里来的？一起玩喽。”
这个事情让我知道，语言不通还要一起好好玩耍，简直就是个灾难！
计量经济学的疯言风语
有一部经典的二战电影《风语者》，讲的是战争双方的密码攻防。美军为了通讯安全，专门雇请神秘的印第安部落纳瓦霍人参军，使用纳瓦霍人的语言进行通讯。因为纳瓦霍语是一种没有文字，只通过世世代代口耳相传，极其复杂的语言，可以说就是不为人知的、偏远地带的“鸟语”。由于他们的语言发音来自于大自然，所以给他们的外号就叫做“风语者”。
哪怕具备了一定的统计学知识，我相信大部分人一开始学习《计量经济学》时也会语言障碍。就好比是日本通讯兵在听美军用纳瓦霍语发送的电报，一头雾水，根本就不带人玩耍的节奏。
下面我就分三个方面来罗列一下计量经济学的三类“疯言风语”：
计量经济学“疯言风语”1：数学符号语言（母语）
数学符号是计量经济学的母语，一点都不为过。其中数学符号主要是搭建了一套共同的语言规则，把社会经济分析中各种含混的概念、术语、各种情景用清晰无误的数学语言表达出来。这样，那些仍旧坚持说自己“方言”的经济学家，自然就不能跟别的小朋友好好玩耍了。
以计量经济学最基础的总体和样本模型定义和内涵为例：
总体回归函数PRF:
\[\begin{align} E(Y|X_i) &= \beta_1 +\beta_2X_i && \text{(PRF)} \end{align}\]
总体回归模型PRM:
\[\begin{align} Y_i &= \beta_1 +\beta_2X_i + u_i && \text{(PRM)} \end{align}\]
样本回归函数SRF:
\[\begin{align} \hat{Y}_i =\hat{\beta}_1 + \hat{\beta}_2X_i && \text{(SRF)} \end{align}\]
样本回归模型SRM:
\[\begin{align} Y_i &= \hat{\beta}_1 + \hat{\beta}_2X_i +e_i && \text{(SRM)} \end{align}\]
看似一堆数学符号，里面乾坤可大着呐。
英文字母表示变量
希腊字母表示参数，戴个帽子就表示参数对应的估计量。
同样是\(Y_i\)，在总体回归模型（PRM）里和样本回归模型（SRM）却是不等价的（为什么？）
总体回归模型里的随机干扰项要用\(u_i\)表达，但是到了样本回归模型里的残差则要用\(e_i\)表达。为什么呢？而且最糟糕的是，国内还有著者习惯把随机干扰项表达成希腊字母\(\mu_i\)，这个简直就是计量经济学语言世界里最容易引起小伙伴惶恐的、不规范的“鸟语方言”！为什么这么说呢？因为大家在概率论与数理统计里都学过了，正态分布由期望和方差两个参数决定\(Z_i \sim N(\mu, \sigma^2)\)。还记得我们前面说好的么：希腊字母表示参数的啊，语言规范可不能说变就变的吧！试想一下，如果你要表达“随机干扰项服从正态分布”，那岂不是一个捉急！（\(\mu_i \sim N(\mu, \sigma^2)\)!!!!）
简言之，计量经济学语言用数学符号来规范用语，并形成普遍共识，大家理解起来就不会相互打架。
计量经济学“疯言风语”2：回归报告语言（暗语）
好吧，只要数学符号能让计量经济语言更加精准一直，大家似乎也能稍微接受这些“枯燥”的数学记号和“不为常人所知”的表达规则了。
不过我们还会碰到第二个语言拦路虎！那就非属哪些惊为天书般的“计量经济分析报告”了！你见过医院里化验科或检验科出具的哪些成沓的身体检查单没？对，就是这些外人看不懂的鬼画符天书！！
先来看一个EViews软件出具的多元回归分析报告吧：
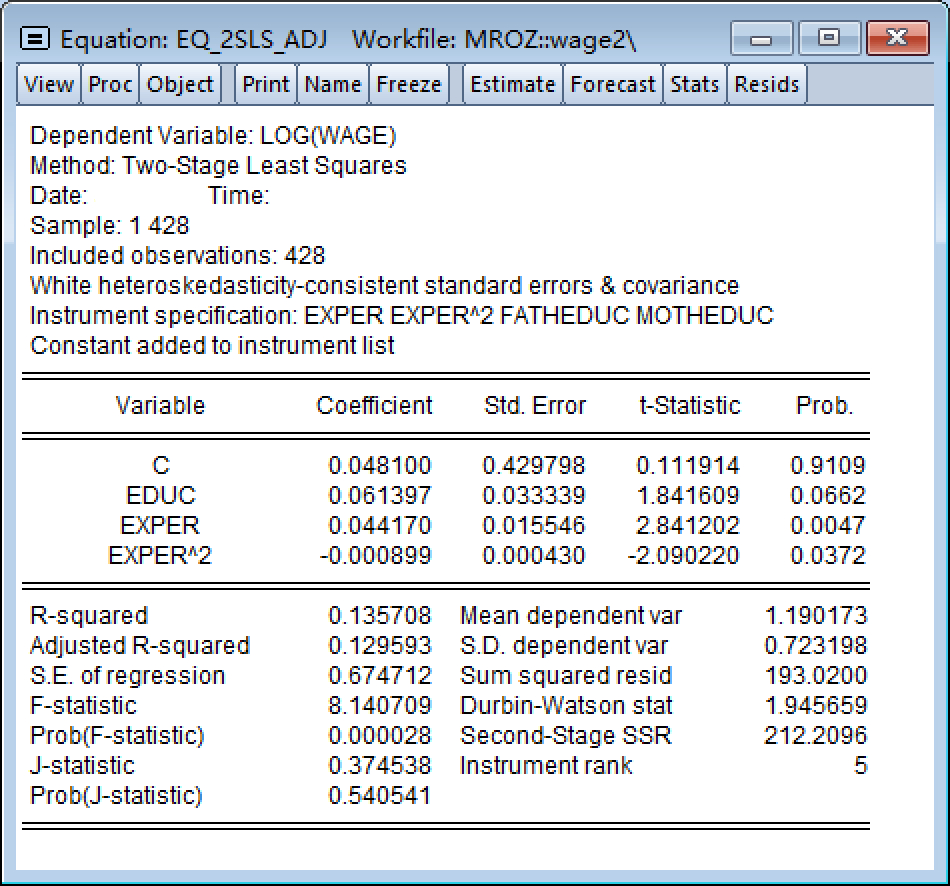
一个多元回归分析Eviews报告
再来看一个R软件出具的两阶段最小二乘法（2SLS）回归分析报告吧：
systemfit results
method: 2SLS
N DF SSR detRCov OLS-R2 McElroy-R2
system 222 213 109.612 0.107301 0.094242 -0.597812
N DF SSR MSE RMSE R2 Adj R2
eq1 111 105 52.0903 0.496098 0.704342 0.139124 0.098130
eq2 111 108 57.5218 0.532610 0.729801 0.049360 0.031755
The covariance matrix of the residuals
eq1 eq2
eq1 0.496098 0.396138
eq2 0.396138 0.532610
The correlations of the residuals
eq1 eq2
eq1 1.000000 0.770653
eq2 0.770653 1.000000
2SLS estimates for 'eq1' (equation 1)
Model Formula: lquan ~ lprice + mon + tue + wed + thu
Instruments: ~mon + tue + wed + thu + stormy
Estimate Std. Error t value Pr(>|t|)
(Intercept) 8.5059113 0.1661669 51.18896 < 2.22e-16 ***
lprice -1.1194169 0.4286450 -2.61152 0.0103334 *
mon -0.0254022 0.2147742 -0.11827 0.9060766
tue -0.5307694 0.2080001 -2.55177 0.0121574 *
wed -0.5663511 0.2127549 -2.66199 0.0089895 **
thu 0.1092673 0.2087866 0.52334 0.6018373
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.704342 on 105 degrees of freedom
Number of observations: 111 Degrees of Freedom: 105
SSR: 52.090321 MSE: 0.496098 Root MSE: 0.704342
Multiple R-Squared: 0.139124 Adjusted R-Squared: 0.09813
2SLS estimates for 'eq2' (equation 2)
Model Formula: lquan ~ lprice + stormy
Instruments: ~mon + tue + wed + thu + stormy
Estimate Std. Error t value Pr(>|t|)
(Intercept) 8.62835440 0.38897023 22.18256 < 2e-16 ***
lprice 0.00105931 1.30954697 0.00081 0.99936
stormy -0.36324606 0.46491248 -0.78132 0.43632
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.729801 on 108 degrees of freedom
Number of observations: 111 Degrees of Freedom: 108
SSR: 57.521843 MSE: 0.53261 Root MSE: 0.729801
Multiple R-Squared: 0.04936 Adjusted R-Squared: 0.031755 以上两个分析报告，局外人自然是云山雾罩，头大不已，真是应了那句老话“隔行如隔山”！
简言之，计量经济学充满了此类“暗语”——各类计算软件的统计分析报告。他们是在各种精致的计量理论下，衍生出来的各类分析方法、诊断工具、统计手段的软件结果的视觉呈现！这里面有蕴含着诸多数学家、统计学家、经济学家大神们的天才设计、神思妙想。然后我们借助神奇的“计算机”，分分钟把天才们的洞见给呈现出来了。这个暗语难于解读，主要在于两点：（1）天才们的思想我们难以领会，或者天才们太多，或者天才的奇思妙想太多！所谓机关算尽，不达目的誓不休！（2）计算分析软件种类繁多，呈现方式各异，处处都是“技术黑箱”（blackbox），无疑又是新手们需要面对的一个个“巨坑”！
计量经济学“疯言风语”3：矩阵语言matrix（狂语）
看过以上两条计量经济学“疯言风语”，估计暗地里给自己使劲加油，必须要鼓足满满的学习勇气了！而下面这第三条计量经济学“疯言风语”，对于很多人而言，简直就是不可逾越的“认知障碍”！
传说计量经济学家都开始抓狂痴怪了，上帝说他们需要清净一下！于是给了计量经济学家一件法宝，那就是“矩阵理论”。
计量经济学“疯言风语”3——矩阵语言matrix（狂语）。矩阵理论运用在计量经济学中，能把高维繁杂的代数问题，转换为紧凑简洁的矩阵语言。这既是语言形式上的一次完美变身，更是思维视野上的一次大跳跃！矩阵点睛，化石成金！
难的是各种矩阵术语和关系式表达扑面而来：矩阵、方阵 对角阵、行列式、秩、列满秩、特征根、转置、逆矩阵、内积和外积、正定矩阵……。
下面给大家展示二元回归下，分别用代数语言和矩阵语言分别求解回归系数的结果。
总体回归模型为，待估计参数包括\(\beta_1,\beta_2, \beta_3\)，假定它们的OLS估计值分别为\(\hat{\beta}_1,\hat{\beta}_2, \hat{\beta}_3\)
\[\begin {align} Y_{i}=\beta_{1}+\beta_{2} X_{2 i}+\beta_{3} X_{3 i}+u_{i} \end {align}\]
下面是用代数语言下OLS的求解结果：
\[\begin{cases} \begin {align} \hat{\beta}_{1} &=\overline{Y}-\hat{\beta}_{2} \overline{X}-\hat{\beta}_{3} \overline{X}_{3} \\ \hat{\beta}_{2} &=\frac{\left(\sum y_{i} x_{2 i}\right)\left(\sum x_{3 i}^{2}\right)-\left(\sum y_{i} x_{3 i}\right)\left(\sum x_{2 i} x_{3 i}\right)}{\left(\sum x_{2 i}^{2}\right)\left(\sum x_{3 i}^{2}\right)-\left(\sum x_{2 i} x_{3 i}\right)^{2}} \\ \hat{\beta}_{3} &=\frac{\left(\sum y_{i} x_{3 i}\right)\left(\sum x_{2 i}^{2}\right)-\left(\sum y_{i} x_{2 i}\right)\left(\sum x_{2 i} x_{3 i}\right)}{\left(\sum x_{2 i}^{2}\right)\left(\sum x_{3 i}^{2}\right)-\left(\sum x_{2 i} x_{3 i}\right)^{2}} \end {align} \end{cases}\]
下面是则是矩阵语言下OLS的求解结果：
\[\begin{align} \boldsymbol{\hat{\beta}} &=\boldsymbol{(X'X)^{-1}X'y} \end{align}\]
二者谁更简洁？两个世界，那个更清净？相信一上台即有分晓。
后话：语言障碍还是心理障碍
与计量经济学的交锋，往往同时夹杂着计量经济学的“疯言风语”语言障碍，以及抽象数学、众多经济理论等的认知心理障碍。
然而，随着计量经济学理论的规范化和互联网信息获取的开源化、便利化，学习上的认知障碍和成本正在逐步消减，而“疯言风语”的语言障碍，则需要假以时日，反复训练（跟学英语或者学计算机语言，大抵相似！）。
总之，计量经济学有其一套独特的科学语言，背后更是有无数天才的智慧和思想闪光，需要大家去沉下心去认真感受和领略！
Hu Huaping
Doctor of Agricultural Economic and Management
My research interests include Data Science, Statistics, Agricultural Economics and Management.